Understanding MFI in the context of FACS data
The speed, sensitivity and versatility of flow cytometry are things of beauty, but with great power comes great responsibility. The fact is that with potentially millions of data points accrued over the run of a single sample, finding the best way to compare those data can be daunting. One of the more commonly misunderstood and often misleading tools in FACS analysis is a pesky little statistic — MFI.
What is MFI?
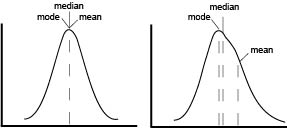
 The first point of confusion is born from the name itself. MFI is often used without explanation, to abbreviate either arithmetic mean, geometric mean, or median fluorescence intensity. In a perfect world, our data would be normally distributed and in that case means, median and mode are all equal. In reality, flow data is rarely normal and never perfect. The more that the data skews, the further the mean drifts in the direction of skew and becomes less representative of the data being analyze as seen on the graphical representation.
The first point of confusion is born from the name itself. MFI is often used without explanation, to abbreviate either arithmetic mean, geometric mean, or median fluorescence intensity. In a perfect world, our data would be normally distributed and in that case means, median and mode are all equal. In reality, flow data is rarely normal and never perfect. The more that the data skews, the further the mean drifts in the direction of skew and becomes less representative of the data being analyze as seen on the graphical representation.
Because fluorescent intensity increases logarithmically, arithmetic mean quickly becomes useless to generalize a population of events, as a right-hand skew causes even more exaggeration of the mean. To combat this, geometric mean (gMFI) is often used to account for the log-normal behavior of flow data, however, even gMFI is susceptible to significant shifts. This leaves us with the median or the mid-point of the population. Median is considered a much more robust statistic in that it is less influenced by skew or outliers. Is there a “right” MFI to use to analyze flow data? No. But generally speaking, median is the safest choice and usually most representative of a “typical” cell.
Three common mistakes when using MFI
Characterizing a bi-modal population: Any average only holds true for normal distributions, and a bi-modal population is by definition not normal. Statistics aside, gating each population and presenting percentages will yield data that is both more easily interpretable as well as more statistically significant.
Comparing data from disparate experiments: Because fluorescent intensity is sensitive to experimental condition (e.g. antibody dilution, tandem dye degradation, laser fluctuations, etc.), it is dangerous to compare intensity of any kind across multiple experiments.
Blindly using MFI as a quantification of expression: While FACS is more than sensitive enough to provide estimates of ligand abundance, such calculations require normalization and calibration using a standard curve. Additionally, it is tempting to say that a population with a higher MFI has higher expression than one with a lower MFI, however, care must be taken to ensure other factors are not responsible. For example, a large cell with more membrane and consequently more surface protein, can appear brighter than a smaller cell of the same type. Thus, it is important to control carefully for things such as size or compensation that may confound results.
So, when should I use MFI?
Not until asked by a reviewer.
Kidding.
MFI has many important uses, but can sometimes be as much a distraction from the data as it is a clarification. Ultimately, like any piece of data, MFI should only be applied if you are absolutely certain that it is the best comparison to make, otherwise it is simply clutter on an otherwise clean histogram.
For further reading:
Flowjo’s excellent explanation of the differences between mean, median and mode. http://flowjo.typepad.com/the_daily_dongle/2007/10/mean-median-mod.html
An amazing article explaining when and why to use bi-exponential axes. Importantly, the affect scaling can have on actually visualizing the median value of a population.
http://facs.scripps.edu/ni0706-681.pdf
 Adam Best is currently a post-doctoral fellow at the University of California, San Diego where he also received his Ph.D. in Biomedical Sciences. His research focuses on understanding the transcriptional events that govern the formation of memory T cells
Adam Best is currently a post-doctoral fellow at the University of California, San Diego where he also received his Ph.D. in Biomedical Sciences. His research focuses on understanding the transcriptional events that govern the formation of memory T cells